最后更新: 2025.12.23

简介

欢迎阅读这份桥式复原法入门教程！本教程假设读者此前没有了解过魔方有关的知识，另外也适合有一定基础（层先法、CFOP等方法）的玩家阅读。

桥式解法蕴含着一些独特的复原思路，因此即便你最终没有选择桥式解法作为主力解法，桥式有关的知识仍然会对提升你的解法有益处。

桥式解法

在一切开始之前，先简单认识一下桥式解法吧：

桥式（Roux）解法是三阶魔方的一种复原方法，以其发明者Gilles Roux（法国）的名字命名。2003年夏，Roux在学习CFOP解法时被其繁杂的公式困扰，决心发明一种简单高效的解法。经Roux本人和其他众多魔方爱好者的完善，桥式解法逐渐发展为一种成熟的速拧方法。它的特点是还原步数少、转体少、公式少，并在最后一步（后六棱）中大量使用 M 层转动，在单手项目上有独特的优势。

所谓M层转动，指的是将左、右两面中间的夹层单独转动：

桥式解法分为左桥（FB, First Block）、右桥（SB, Second Block）、四角归位(CMLL)、后六棱(LSE, Last Six Edges)4个步骤。

左桥

复原一个1×2×3的块（左桥）。

右桥

复原另一个1×2×3的块（右桥），位置与已有的左桥相对。

CMLL

复原顶层的四个角块的朝向和相对位置。

后六棱

复原最后六个棱块，即位于顶层的左右两侧各一个棱块，以及M层的四个棱块。

如何使用本教程

虚拟魔方

本教程提供了大量的虚拟魔方演示，可以拖动以改变朝向；对于带有转动的演示，点击它们以执行转动（注意在第一次点击之前，它们显示的状态有可能是最终状态）。虚拟魔方的下方还有单步执行、恢复初始状态等选项。

建议使用电脑端阅读本教程，以更方便地观察这些虚拟魔方。如果使用手机端，尽量不要拖动虚拟魔方，因为拖动操作并不稳定；一些图片在竖屏下可能会变窄，可将手机切换为横屏阅读。

复原步骤的阅读

本教程采用总分的结构，共有三章（不包括记号）。每一章的开头会介绍对应步骤的复原目标，并给出图片形式的简略教程。每章下的小节则会详尽介绍对应步骤的做法。对于有一定基础或者理解能力强的读者，你可以只阅读章前的内容，而跳过小节中的详尽介绍。如果你已经完整学习了一遍，而忘记了某个情形的做法，有时也能通过章节开头的复原指引快速查阅。

桥式复原法中，每个阶段都有很多种可能的情形(case)，因此会涉及到分类讨论。在阅读每个小节时，你不必逐句阅读，而是可以先像查字典一样，根据你手中的魔方对应的情形，只阅读所需要的部分。完成这一阶段的复原后，直接跳到下一阶段，直至还原好你手中的魔方。经过多次的重复打乱和复原，你将逐渐学会应对每一种可能的情形。

如果某种情形难以通过打乱遇到，你可以使用逆转动的方法得到这一情形。

入门

本节简单介绍魔方的基本知识。

基础知识

你现在手中拿着的魔方被称为三阶魔方，因为它呈立方体形状，且每一条棱上包含三个块。三阶魔方的块分为三类：

角块
- 角块拥有3个面，出现在立方体的每个顶点上，总共有8个。
- 无论怎样打乱魔方，同一角块的三个面之间的相对位置不会变化。
棱块
- 棱块拥有2个面，出现在立方体的每条棱的中央，总共有12个。
- 无论怎样打乱魔方，不同类型的块不会相互转换。例如，角块不可能移动到棱块的位置上去。
中心块
- 中心块拥有1个面，出现在立方体的每个面的中央，总共有6个。
- 无论如何打乱魔方，中心块之间的相对位置不会变化。例如，在标准配色下，白色中心块的对面一定是黄色中心块。

这三类块构成了立方体表面上所有的26个块。

标准配色

请检查你手中的魔方是否是标准配色，这是本教程能够顺利指导复原的前提。方法是观察各个面上的中心块，无论魔方是否为打乱状态。原则如下：

白对黄（白色中心块的对面是黄色中心块）、蓝对绿、橙对红。
如果面朝黄、绿、红的三个中心块，它们将依次按顺时针排列。

尝试还原

你可以尝试自行复原魔方的一面：

或者更进一步，一层：

记号

本节的内容多且重要，但这不意味着你需要一次性记住。后续章节中出现记号时，往往伴随着虚拟魔方的转动演示，你可以将动画与记号对应起来。对于桥式解法，最重要的几个转动记号为U、F、R、M与r。

位置

一般来说，我们在复原中会选一个面对准自己。一旦视野中面积最大的面（称为“前”面）选定，并且魔方姿态正直，那么魔方的朝向也就确定了。视野中至多只能同时看见“前”面周围的两个面。

按照视野中各个面的不同朝向，采用以下记号来标记它们：

顶，或U（Up），有时也称为上
前，或F（Front）
右，或R（Right）
底，或D（Down，与U相对）
左，或L（Left，与R相对）
后，或B（Back，与F相对）

在下图中的朝向中，各个面与中心块的对应关系为：U-黄、F-红、R-绿、D-白、L-蓝、B-橙。

务必注意，面的记号代表的是这个面所处的方位，是由魔方的朝向决定的，而不是中心块的颜色。魔方的朝向改变时，面与中心块颜色的对应关系也会改变。在本节中，任何记号都不与某种特定的颜色相对应。

因此，请避免改变本节中所有虚拟魔方的初始朝向，否则记号无法与演示相对应。

由于棱块存在于两个面的交界处，因此使用两个面的记号也可以唯一表示棱块的位置。UR位指的是U面与R面交界的位置，在下图中为橙绿棱块。这里只表示块的位置而不表示朝向，因此字母之间的顺序是随意的。

处于同一位置的棱块，有两种不同的朝向可能。

角块的位置也可同理表示。下图中的黄红绿棱块位于URF位。

单层转动

试着转动魔方。魔方的所有6个面都可以转动，且每次转动都有一个面唯一对应。因此，转动记号可以沿用上节中的关于面的位置记号。

根据效果的不同，用三种记号来表示同一个面的转动：

大写字母（顺时针转动90°）
大写字母 + ' （逆时针转动90°）
大写字母 + 2 （旋转180°）

例如，U不仅表示顶面，也表示顶面按照顺时针旋转90°。U'则表示将顶面按照逆时针旋转90°。U2和U'2的效果相同，都是将顶面旋转180°。

使用下面的动画，点击中间的运行按键来熟悉每个转动记号，并且同时试着与你手中魔方的转动联系起来。

U 转动

L 转动

F 转动

R 转动

B 转动

D 转动

B层、D层和L层的转动方向也许有些特殊。注意所谓的顺逆时针，都是假定直接面向这个面的来观察的，而不是从你的视角的位置。例如，D’表示你从魔方底部向上看时，底层向逆时针旋转90°。U’和D’都代表逆时针旋转，但从你的角度来看，它们的转动方向是相反的。

应当逐步熟悉所有6类转动的手法，而不要先把要转动的面移动到自己面前，再去转这个面。即使这个面在视野之外（如转动B’），也不要改变魔方的朝向。

转动序列

形如R U R' U'的转动记号组合，代表依次进行对应的转动操作。

(R U R' U')2则代表将括号中的转动序列执行2次。它等价于(R U R' U') (R U R' U')或是R U R' U' R U R' U'。

括号有时是为了方便记忆而设置的。

逆转动

将R U R' U'倒过来做，对应的转动是U R U' R'。逆转动是这样得到的：先将R U R' U'的记号倒过来，得到U' R' U R，再改变每个记号的顺逆时针。当然，如果是U2改变为U'2，可以不改变写法。

本教程中出现的转动序列，都是用于将打乱状态转为复原状态。你可以从已复原的状态出发，通过逆转动得到对应的初始情形(case)。

转体

转体就是魔方的整体转动。魔方可以通过三个基本的维度进行转体，因此使用所围绕的坐标轴来表示不同的转体。注意下面的y与z转动，与右手坐标系的y、z轴是相反的。

更简单的记忆方法是记住对应的面： x, y和 z 分别对应 R, U和 F 的方向。例如，转体x' 和转动 R'类似，与R面平行的每个层都向同样的方向转动。

x 转体

y 转体

z 转体

桥式解法无需转体。为了便于入门，本教程的最后一个步骤将用到一些x转体。在进阶阶段，它们可以被无需转体的方法替代。

其他有用的记号

使用转动和转体记号的组合，就足以表示所有的转动了。但也有一些组合转动，在桥式解法中会非常有用：M、r。E、S在特定情形下也许也会用到。

M转动

M层指的是L、R层中间的夹层，而M指的是将M层转动，而保持两边的层不动。M层转动可以作为桥式解法的一大特色。M层的顺逆时针的方向判断与L一致。你可以这样记忆：M字母中间的“V”指向下，这就是M转动的顺时针方向。

应当逐步练习一次性完成对M'或M的转动，不能用两次转动来代替。你可以使用左手无名指，从魔方下方推动M'。转动M也可通过左手无名指从魔方下方反推来完成。如果觉得比较困难，可以先用其他手指，从魔方上方将M层“压下去”。（为了M层转动的顺畅，建议使用一个好一些的魔方！）

虚拟魔方对M2和M'2未做区分。实际转动时，做M'2，即做两次M'，会更加方便。

r转动

r转动指的是在转动R层时，连带将M层转动。因此其顺逆时针的方向判断与R一致，但采用小写表示双层转动。注意r等价于转动L和转体x的叠加，不要混淆r与L。

Rw记号在三阶魔方中等价于r。该记号通常用于高阶，其中的 w 代表的是“wide“（宽）。如果在其他教程中遇到，知道它们是一回事就好。

不确定的转动

在本教程中，有时只能确定旋转哪一层，而具体旋转的效果要视情况而定。为了解决这类情况下表示的困难，约定采用“字母+x“来表示这类转动的集合。例如，用Ux来表示U层的所有可能转动，它可能是U、U2、U’，甚至U0（不转动）。同理有Rx、Mx、rx等。

冷门记号

E转动

E层指的是U、D层中间的夹层，对应的转动为E转动，其顺时针转动方向与U一致（也和字母“E”的开口方向一致）。在桥式解法的最后一步中，有的玩家会使用双手E转动，处理一种称为“四心换”的情形。

S转动

S层指的是F、B层中间的夹层，对应的转动为S转动，其顺时针转动方向与F一致。在单手处理“四心换”情形时，有的玩家会使用S转动代替E转动。

两桥

“两桥”指的是左桥和右桥。“桥”指的是一个1×2×3的块，按照摆放的位置区分为左桥和右桥，位置相对。复原顺序是先左桥，后右桥。

以下是一个已经复原好的左右桥：

如复原步骤的阅读所述，每章开头的部分会给出图片形式的简略教程，以下部分大致了解即可。你也可以跳过，在后续的章节中再详细学习。

复原步骤

左右桥的复原过程非常自由。一种可行的复原步骤如下：

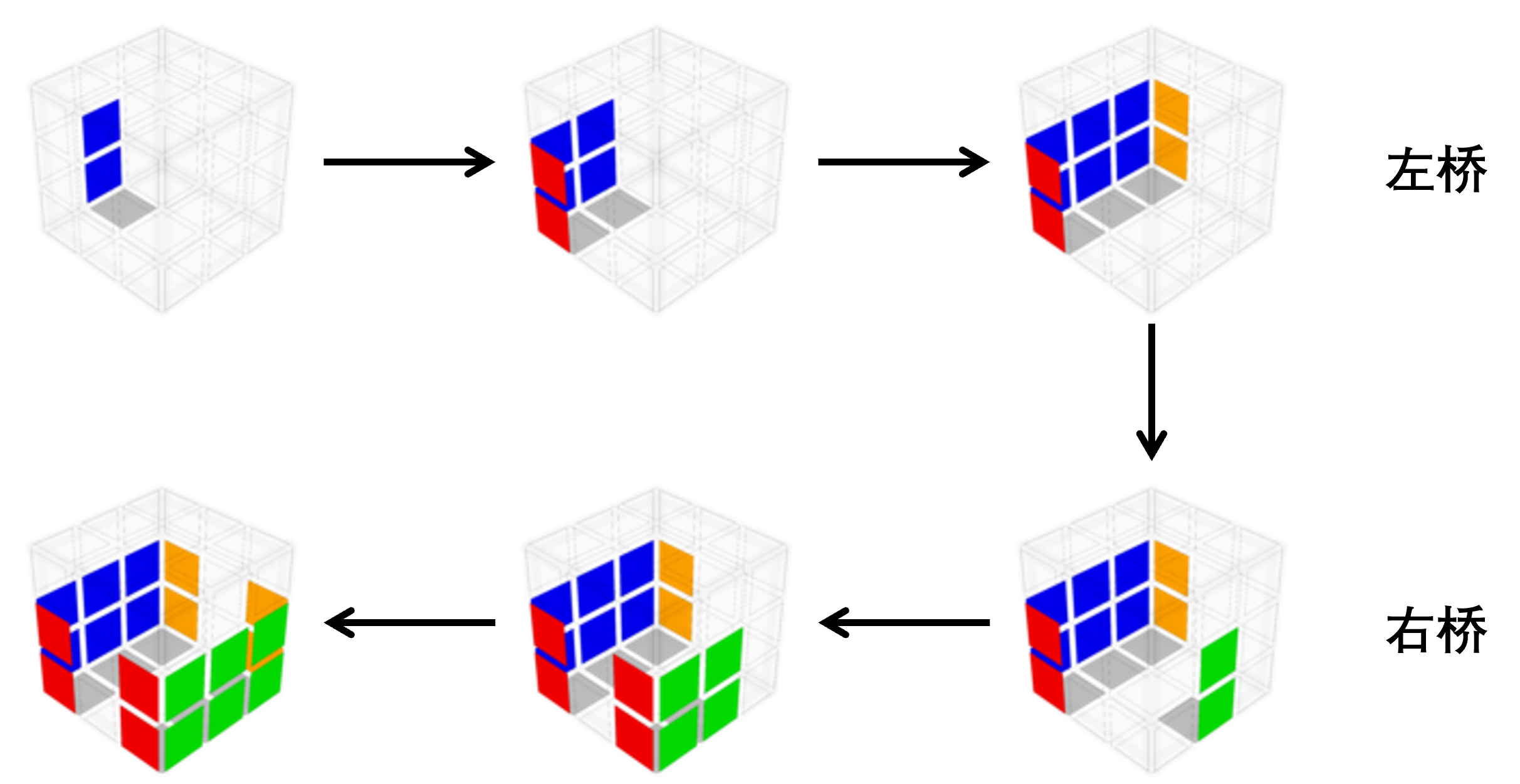
每个桥的复原都是先完成底层的棱块，再完成两侧的棱块与角块的组合（棱角对）。

棱角对复原

棱角对的复原是两桥部分的重点，其复原过程也较为自由。一种可行的复原过程如下：

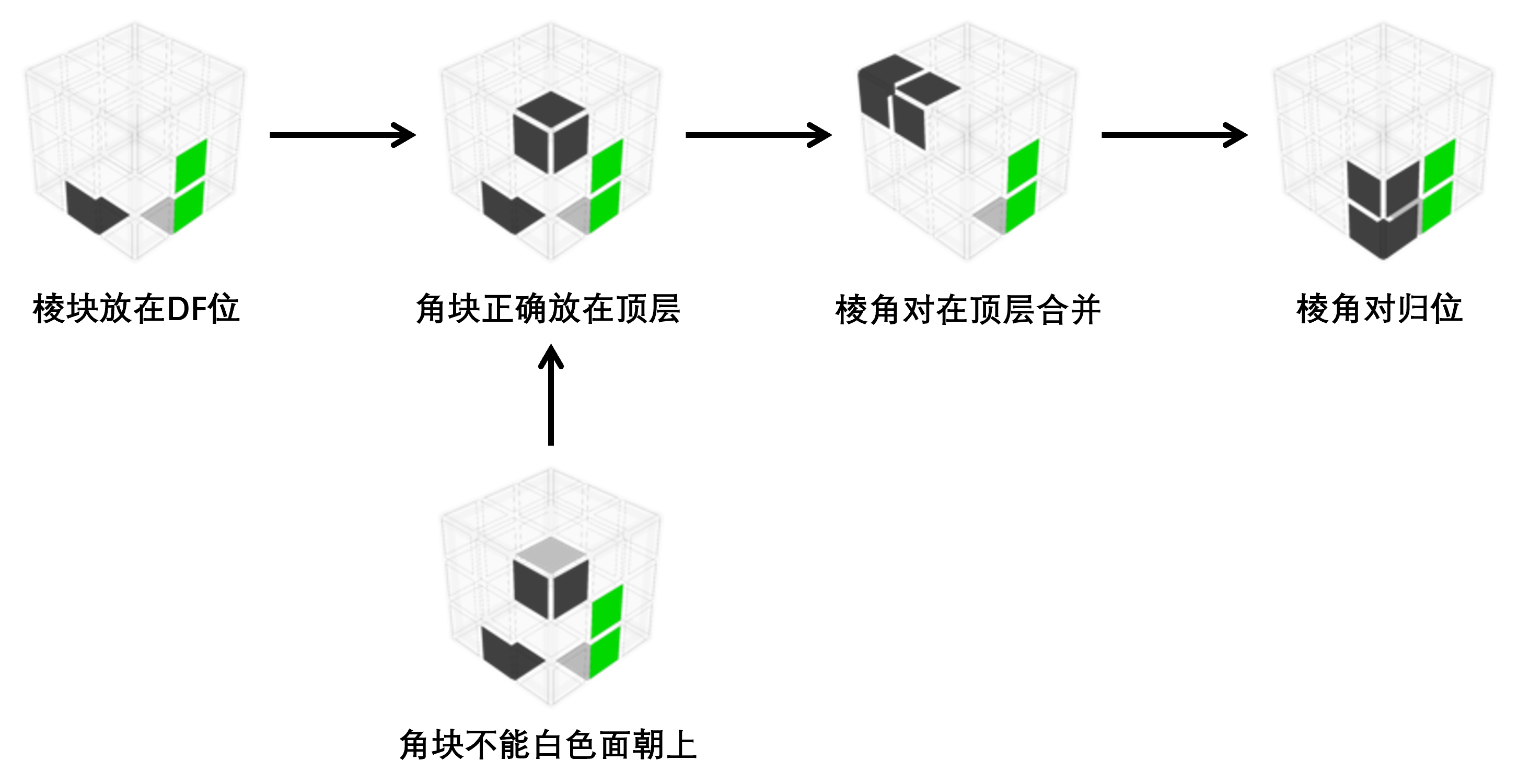
仅作为示意，棱角对的位置不必一致。

左桥棱角对的复原只会比右桥的更简单。对于右桥的另一棱角对，你可以通过将操作做前后镜像，完成复原。

两类基本操作

在完成右桥时，两类基本操作R Ux R'与R' Ux R会非常有用：它们涉及与右桥空缺棱角对的位置有关的块的操作。可以将空缺棱角对的位置中的块移出，或是将位于顶层的棱角对放在空缺棱角对的位置中，完成归位。

它们也可以对UFR位或UBR位的角块做翻转，调整角块的朝向。通过这种方法，可以使待复原角块的白色面不朝上。例如：

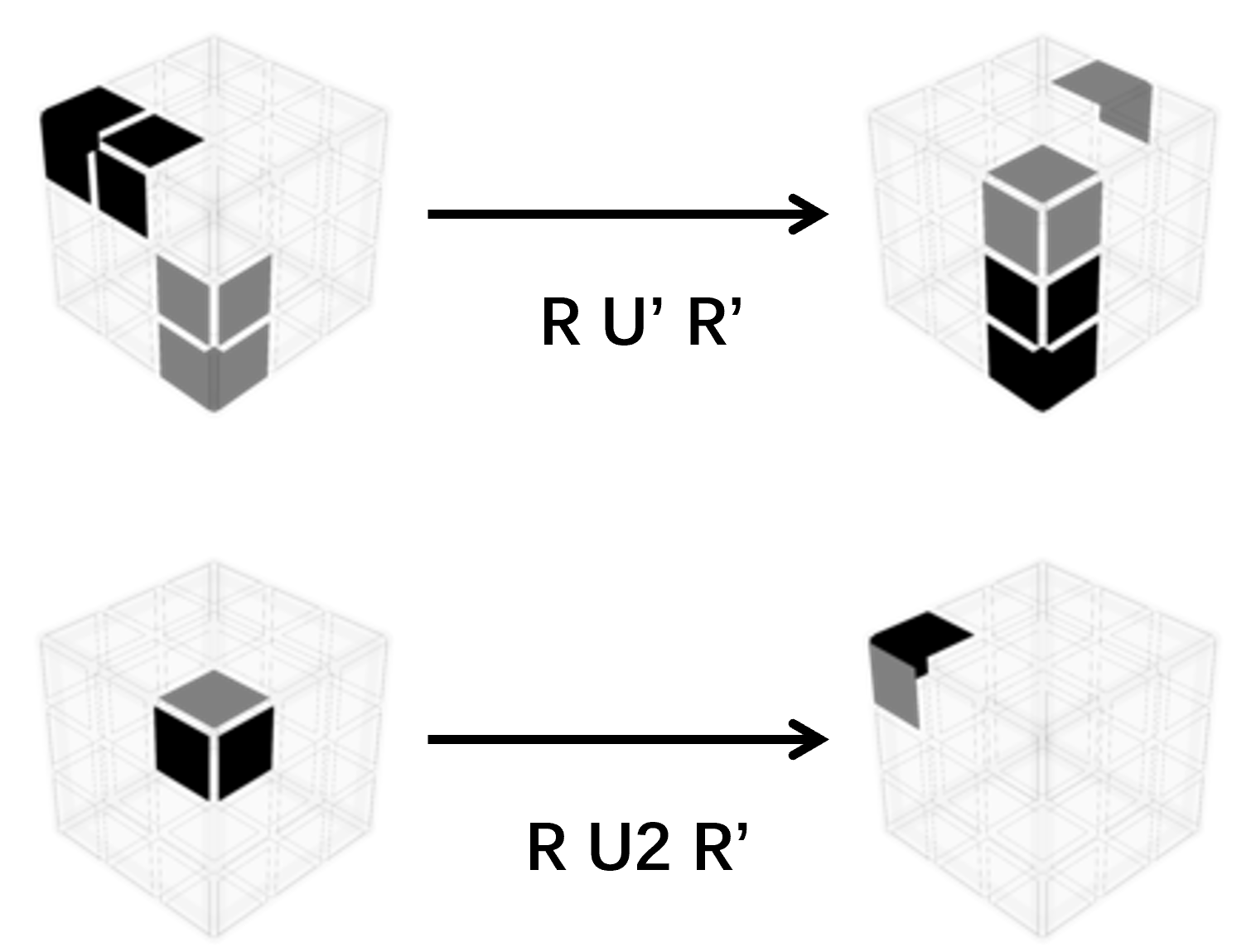
左右桥的具体内容将在以下两节介绍。若上面的简略复原指引已经足以让你理解并复原左右桥，你也可以跳过后面的详细介绍。

左桥

目标

左桥是一个1×2×3的块，其中2×3的面的颜色就称为这个桥的颜色，1×3的面的颜色称为这个桥的底的颜色。

左桥作为一个步骤，指的是把魔方左侧的1×2×3的块复原，作为桥式的第一步。左桥有24种可能的选择，但本教程将始终将白色底的蓝色桥作为待复原的左桥，并且后续的复原都以此为基础。

下面是一个白底蓝桥的形态，你可以拖动魔方以仔细观察。

你可以借鉴复原一层的思路来复原左桥，例如先组好一部分十字，再插入对应角块。但仍然推荐你通过下面的内容，理解构筑、插入棱角对的思想。这个思想也应用在右桥的复原中。我们只介绍最笨拙的左右桥复原方法。如果已经学会了如何通过组棱角对复原左桥和右桥，你可以大胆探索：是否能够走不一样的复原流程？是否可以用更少的步数完成同样的目标？

1 复原底棱

第一步是将蓝色中心块与蓝白棱块合并。合并后，蓝白棱块的蓝色面应当与蓝色中心块相邻，而白色面朝下。

首先调整中心块朝向。旋转魔方，使得蓝色中心块位于左面。相应地，绿色中心块会位于右面。

此后，始终让蓝色中心块位于左面，直到整个魔方复原。

只需调整蓝绿中心块的位置。在桥式的最后一步（后六棱）以前，其他中心块的位置不需要关心。

调整朝向后，将蓝色中心块与蓝白棱块合并，并使白色面朝下。这步至多通过两次转动就能完成，以下是一些实例。

例1: D层转动

例2: 未归位，朝向错误

例3：归位，朝向错误

有很多可能的解法，请自行尝试。

完成后，为了不改变蓝绿块的位置，此后我们不会轻易转动L层或D层。

2 复原一对棱角对

接下来要完成一个 1x2x2 方块。可以使用蓝红-白或蓝橙-白棱角对，与已有的部分组合起来。

以下是一个由蓝红-白棱角对组成的方块。

棱角对指的是一对正确组对的棱块和角块，其位置任意。AB-C棱角对表示棱块和角块都含有A色和B色，而角块额外含有C色。例如，下面是一对已归位的蓝白-红棱角对：

蓝白-红

根据左桥的复原形态，位于蓝白桥两侧的棱角对，前面的棱角对的侧面颜色是红，而后面的棱角对对应橙。如果在复原过程中不清楚侧面的颜色，可以转动r层(rx)，将白色中心块与已复原的白底棱块对齐，再根据侧面的中心块颜色判断。

例如，根据中心块颜色可以看出，左桥为橙黄桥时，前棱角对的侧面颜色是绿。

如前面所述，白色中心块不需要始终与白底棱块对齐，因为它接下来可能随着r层和M层转动而不断移动。

为了复原蓝红-白棱角对，我们采用以下步骤：

2-1 棱块放至起始位

起始位指的是是DF位，用黑色标出。

这一步的目标是将蓝红棱块放在起始位，不关心其颜色的朝向。步骤如下：

通过Ux、Fx或Bx，将蓝红棱块放在M层。随后做rx，将棱块放入起始位。

如果棱块已经位于M层，显然不需要通过Ux、Fx或Bx调整。Ux的说法包含了这个意思，因为Ux包含U0。随后的rx也同理。这种隐含的“如果已经完成，可直接跳过”的含义，在后面还会出现很多次，不再单独强调。

特例：棱块处于DR位

此时无法用上述流程解决，做R F即可。

2-2 调整角块色向

这一步的目标是调整蓝红白角块的位置。目标是将蓝红白角块放在顶层，并让白色面不朝上。

大多数情况下，通过Rx或Bx一步就能完成。

特例1：角块已经归位（LFD位）

此时，无论怎样移动都会影响之前棱块的位置。此时做r' F r。

特例2：角块位于LFU位且白色面朝上

此时，先转Ux将角块放在某个翻转位上。

翻转位指的是UFR位或UBR位，用黑色标出。

然后，作R或R'以翻转，将它放到另一个翻转位上，此时白色面便不在顶面上了。

或：

2-3 棱角对归位

这一步的目标是组好棱角对，并和已有的部分合并成方块。

首先做Ux，使白色面移到侧面（L面或R面），具体哪面视蓝红棱块的朝向而定。其次做rx或Rx，将棱角对正确合并。最后通常能通过一步F或F'完成归位。

特例：不能直接F归位的情形

3 复原另一棱角对

接下来将复原剩余一对棱角对，完成左桥构建。在这里，我们需要复原蓝橙-白棱角对。

复原第一对棱角对的经验，可以几乎原封不动地用到第二组棱角对的复原中，因为它们只是关于前后做了镜像。通过下面的例子，你会看到如何用相同的办法复原蓝橙-白棱角对。

3-1 棱块放至起始位

原本的DF位仍然可以作为起始位。下面的例子中，我们选择它的镜像位DB位。

3-2 调整角块色向

将蓝橙白角块放在顶层，并让白色面不朝上。仍然使用了“翻转位”的方法。

3-3 棱角对归位

组好棱角对并归位。Ux rx Bx或Ux Rx Bx'能够处理大部分情况。

组第一组棱角对时，这个步骤的最后一步是Fx。作为镜像操作，这里被换成了Bx。

更多的情形请自行尝试，注意复原时不要破坏已有的方块。

不同的复原步骤

前面已经提到过，我们介绍的方法是非常死板的，实际上，桥式方法中的筑桥非常灵活，尤其是左桥，因此一定要多尝试，而不要拘泥于特定的复原步骤。下面介绍一些不同的思路。

左桥中的1x2x2 方块有前后两种选取方式。我们在复原第一个方块时，选择了位置靠前的方块，为此先复原了前棱角对（蓝红-白）。当然也可以先复原后棱角对，组好后面的方块。

一个1x2x2 方块有两组棱角对。我们先复原了蓝白棱块，再复原蓝红-白棱角对。如果先复原蓝红棱块，再复原相应的蓝白-红棱角对，当然也可行。但这样就提前选定了方块（假设不更改左桥的底色），在组第一个方块时，棱角对的选取只有一种。

更进一步，左桥不必一定按照“一个方块+一对棱角对”的顺序来复原。例如，“三三桥”将左桥分为两个1x1x3的条并分别还原。“S桥”先复原两侧的棱角对，再通过S层转动将中心块与蓝白棱块归位。

右桥

目标

右桥也是一个1×2×3的块，与左桥相同，而位置与左桥相对。其底色与左桥相同，桥色相反，因此需要完成一个白底绿色桥，并且不能破坏已经做好的左桥。

你可以通过下面的已经完成好的右桥，观察它与上节复原的左桥的联系。

1 复原底棱

第一步是将将绿色中心块与绿白棱块合并、归位。

如果绿白棱块已经和绿色中心块对齐，或绿白棱块在顶层且白色面朝上，通过 Ux Rx直接归位。

例1: 直接归位

如果不能通过上面的方法归位，就将绿白棱块转动到M层，并使棱块的白色面朝上，然后再做上述操作。下面给出两个例子。

例2: 棱块在M层

转动rx或Mx即可。

例3：棱块不在M层

转动Rx Ux，将绿白棱块转动到M层；再做rx，使棱块的白色面朝上。

2 复原一对棱角对

接下来要完成右桥中的一个 1x2x2 方块。可以使用绿红-白或绿橙-白棱角对，与已有的部分组合起来。

我们选择复原由绿红-白棱角对组成的方块，如图所示。

我们介绍两类基本操作，以完成和右桥棱角对位置有关的块的处理：

基本操作一：`R Ux R'`

这里的Ux可以是U、U'或U2。作用是将F、R层交界位置的两个块（灰色）移动到顶层。相应地，它们的位置也会被原本在顶层的两个块（黑色）替代。

基本操作二：`R' Ux R`

与基本操作一类似，作用是将B、R层交界的两个块移动到顶层。

为了组好绿红-白棱角对并归位，我们采用以下步骤：

2-1 棱块放至起始位

这一步的目标是将绿红棱块放在起始位（DF位），不关心其朝向。和左桥相同，我们选择DF位作为起始位。

通过Ux将绿红棱块放在M层，然后做Mx，将棱块放入起始位。

特例：棱块在右桥的位置上

如果棱块位于RF位或RB位，使用上面介绍的基本操作，将棱块移动到顶层，此时便位于M层了。

对于RB位，选择基本操作二。（为什么？请回忆基本操作的功能）

在左桥中，我们曾能够用Fx或Bx调整，将棱块移动到顶层。在右桥中不再适用。

2-2 调整角块色向

这一步的目标是调整绿红白角块的位置。目标是将绿红白角块放在顶层，并让白色面不朝上。

首先，将绿红白角块放在顶层。如果它不在顶层，那么一定在右桥位置上（RFD位或RBD位）。此时做一次基本操作即可。这里同样需要根据块的具体位置，以确定使用基本操作一还是二。在基本操作中，对Ux做适当的选择，可以避免做完后角块的白色面朝上的情况，从而一步到位。

同样的情形下，如果选择第二步做U'，将导致白色面朝上，需要额外做翻转。

如果绿红白角块已经在顶层，且白色面朝上，那么需要调整角块的朝向。首先，转Ux将角块放在某个“翻转位”（UFR位或UBR位，见左桥-调整角块色向的特例2）上。

如果在翻转位UFR位，做基本操作一中的R U' R'或R U2 R'。

如果在翻转位UBR位，做基本操作二中的R' U R或R' U2 R。

在左桥中，我们曾能够用一步Rx完成角块翻转。右桥中，Rx会破坏已复原的底棱。

2-3 棱角对归位

这一步的目标是组好棱角对，并和已有的部分合并成方块。

首先做Ux，使白色面移到侧面（L面或R面），具体哪面视绿红棱块的朝向而定。其次做Mx，将棱角对正确合并。

在左桥中，我们曾用rx或Rx，让角块移动。在右桥中，我们反过来让棱块移动，以迎合角块。

合并后有四种可能的情形。

例1 基本操作一

例2 基本操作一，但是双层转动

例3 转化

U2转化为例1。另有一种情形同理转化为例2，不再列举。

3 复原另一棱角对

接下来将复原剩余一对棱角对，完成右桥构建。在这里，我们需要复原绿橙-白棱角对。

和左桥一样，这步可以套用第一组棱角对的做法。

3-1 棱块放至起始位

将绿橙棱块放在起始位，即DF位。

3-2 调整角块色向

将绿橙白角块放在顶层，并让白色面不朝上。仍然使用了“翻转位”的方法。

与复原第一组棱角对不同的是，此时前棱角对已归位，那么应该避免选择基本操作一，因为它会破坏这组棱角对的位置。因此这时翻转位只能选择UBR位，并做基本操作二。同理，如果是先复原后面那组棱角对，那么要避免做基本操作二。

3-3 棱角对归位

组好棱角对并归位。

棱角对正确合并后，这里出现的情形和第一组棱角对归位中的例2互为镜像，因此解法也是镜像的：r与r'对称，U与U'对称。

更多的情形请自行尝试。

顺带一提，在后续的“后六棱”步骤中，将会要求顶层的中心块为黄色或白色。由于整个右桥的复原总是以Rx或rx结尾，因此恰当地选择做Rx还是rx，就能直接调整好顶层的中心块，从而避免通过Mx再次调整。

CMLL

目标

这步要还原顶层的四个角块的朝向和相对位置，如图所示。CMLL的含义是：复原最后一层的角块，而不关心M层的情况(Corners (regardless of M slice) of Last Layer)。

完成后，顶层可以自由旋转，角块不必一定和左右桥对齐。

CMLL步骤中会引入一些公式（在本教程中，指的是4步以上的转动序列）。

你可以选择最少的记忆量（1条公式：公式〇），但会多很多转动步数，并且需要理解如何叠加公式。

你也可以记忆全部9条公式（公式一~三、进阶公式一~六），避免叠加造成多余步数。

在后面两节的介绍中，我们将主要介绍折中的方案（3条公式：公式一~三），并顺带提及前面两种方案。然而，当你对桥式复原法较为熟练之后，建议将9条公式全部掌握。

我们将CMLL分为以下两个步骤：

一. 复原四角色向

这步要将顶层的四个角块在顶层上的颜色还原正确，也就是黄色一致朝上。

叠加法

采用公式一、二的叠加法如下：（以下皆为俯视图）

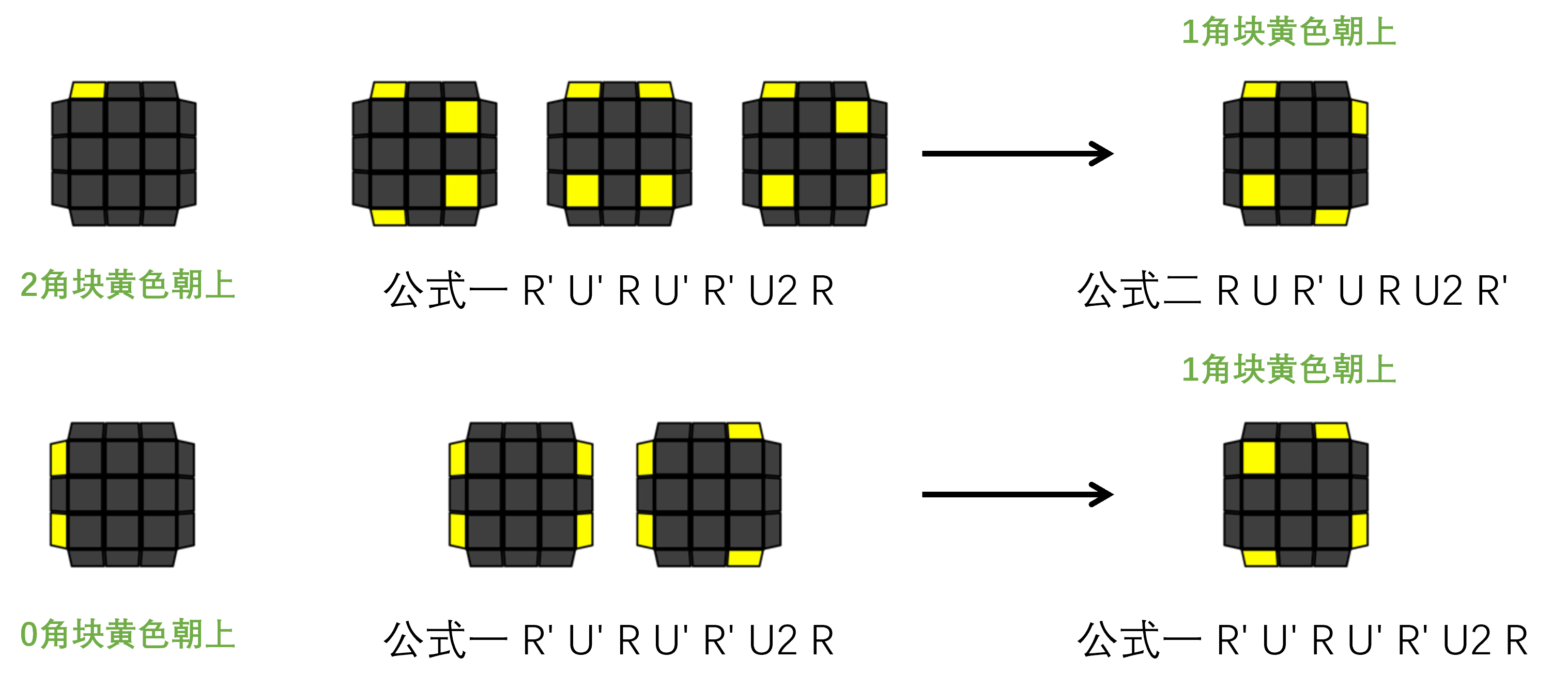
注意，使用公式完成形态转换后，通常还需要做Ux调整朝向。

公式法

直接复原的公式如下：

二. 复原四角相对位置

这步将彻底完成CMLL步骤，也就是将顶层的四个角块的相对位置也还原正确。

公式如下：

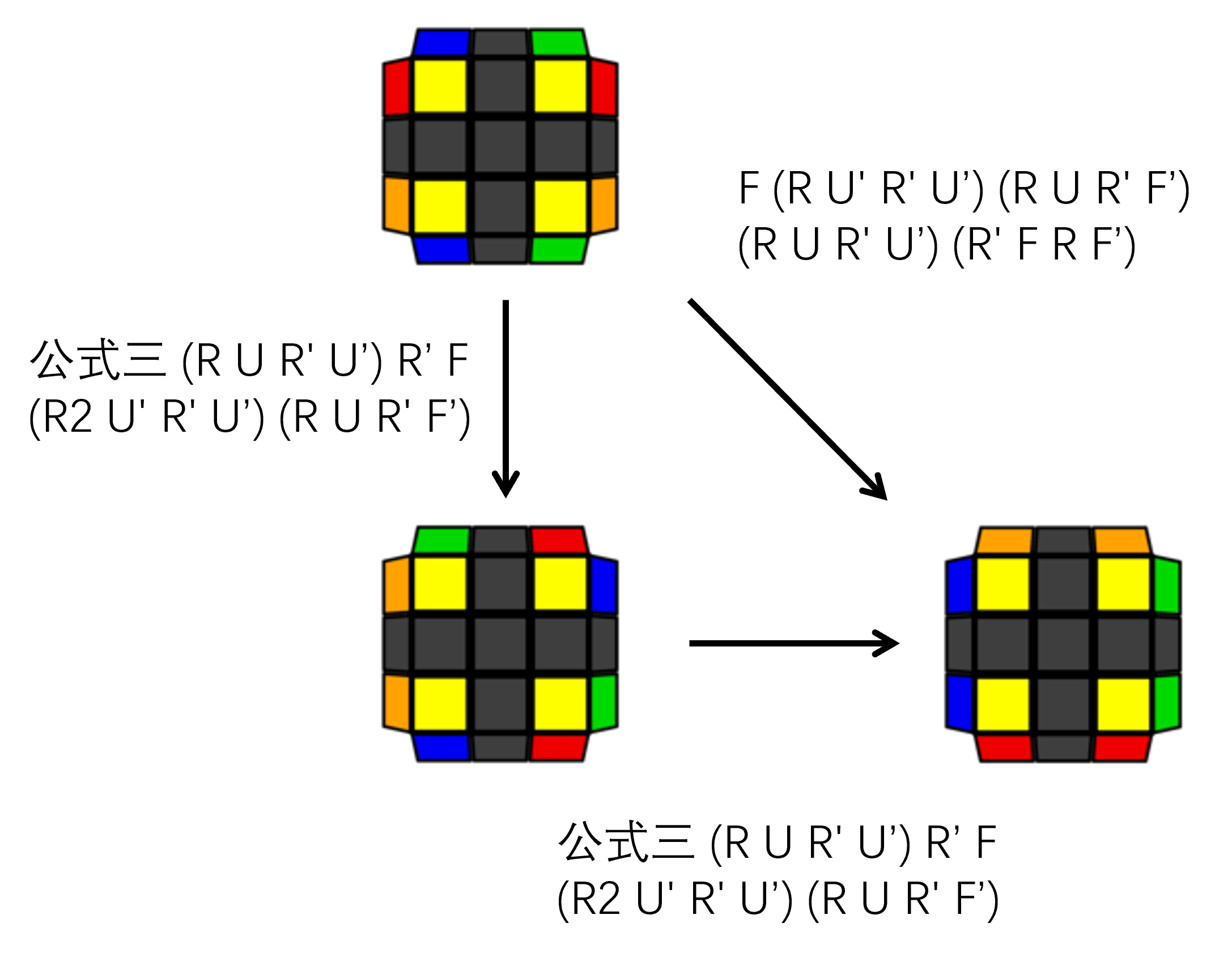
CMLL的两个步骤的具体内容将在以下两节介绍。

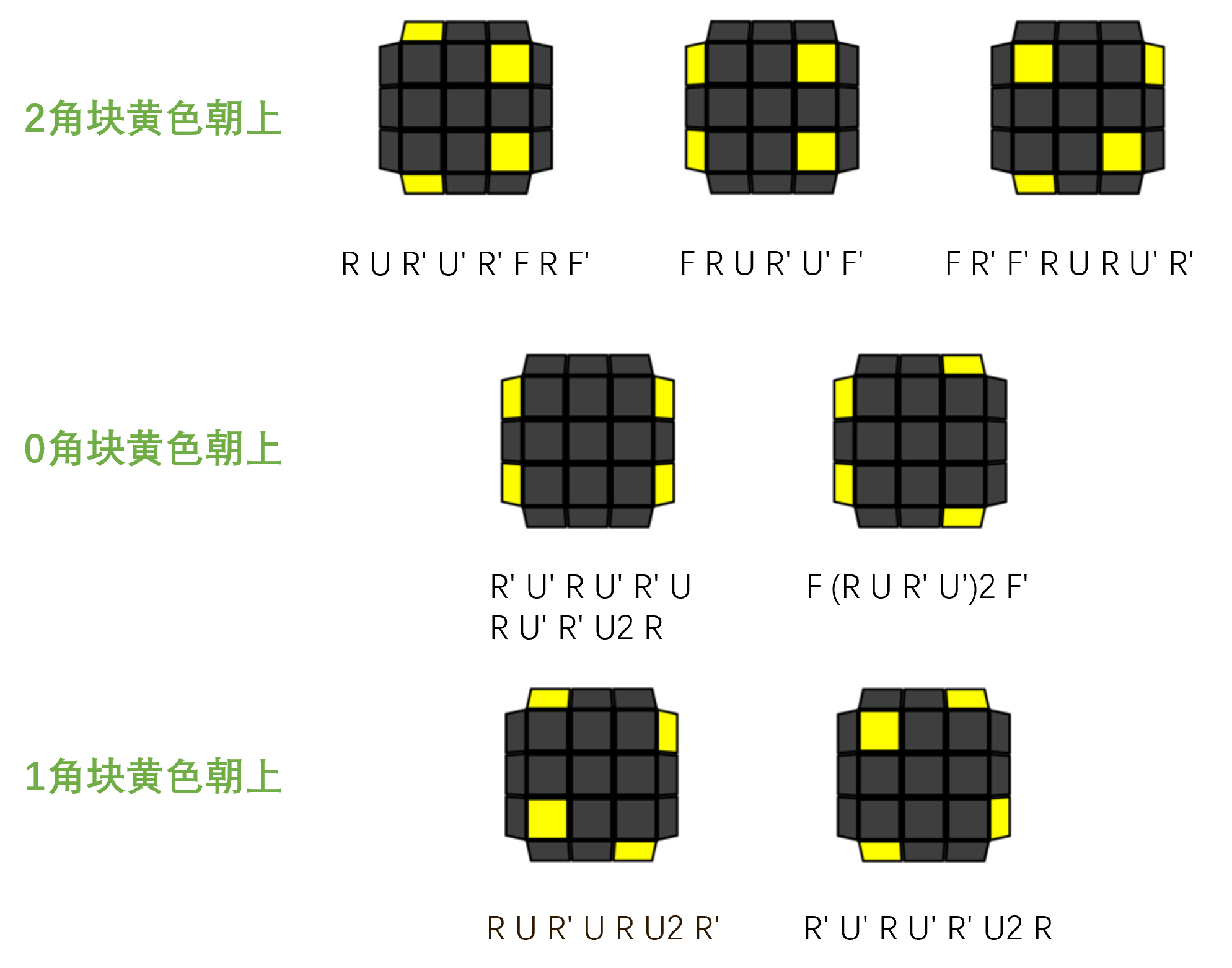
四角色向

这步要将顶层的四个角块在顶层上的颜色还原正确，也就是黄色一致朝上。

共有7种未还原的情形。根据顶层四角的位置上已还原的黄色面的数量，将其分为3类：

一个黄色面已还原

As

上图为As形态的俯视图，特点是3个未复原的黄色面都在对应角块的右侧。换句话说，将角块逆时针旋转120°，可以把黄色面移动到顶层。使用公式前，通过Ux将已复原的黄色面放在俯视图的左上角。

公式一 R' U' R U' R' U2 R

这个公式的组成为：(基本操作二) U' (基本操作二)。（见基本操作二）可以看出，它先将右桥的后棱角对移动到顶层，再换一种方式重新插入。

如果你只想为整个CMLL步骤记忆一条公式，那么记忆下面的公式：

公式〇 R' U L U' R U L'

S

S形态的特点是3个未复原的黄色面都在对应角块的左侧。使用公式前，通过Ux将已复原的黄色面放在俯视图的左下角。

公式二 R U R' U R U2 R'

这个公式的组成为：(基本操作一) U (基本操作一)。（见基本操作一）它对右桥的前棱角对完成重新插入。

也可以只使用公式〇。将已复原的黄色面放在俯视图的左上角位置，再完成：

(公式〇) U' (公式〇)

叠加法

除As与S以外的所有形态，都能通过执行一次公式一转化为As或S形态，因此总能通过叠加前面的公式来解决: Ux (公式一) Ux (公式一/公式二)。Ux用于调整朝向。

也可以只使用公式〇，因为公式一可以替换为公式〇、公式二可以替换为(公式〇) U' (公式〇)。注意中途用于调整朝向的Ux可能有一些变化。

两个黄色面已还原

恰好两个黄色面已还原的情形有3种。其叠加法如下：无论哪种情形，保证俯视图中左上角的角块是黄色朝上的:

然后使用公式一，就一定转为S形态，从而能够通过公式二解决。

下面的T形态中，给出了叠加法的一个具体例子。

T

T形态中，两个未还原的角块相邻，黄色面方向相对。

采用叠加法时，首先保证俯视图中左上角的角块黄色朝上，上图已满足要求。然后，执行公式一。U2调整朝向后，再做公式二。

T形态复原公式：

进阶公式一 (R U R' U') (R' F R F')

U

U形态中，两个未还原的角块也相邻，但黄色面方向相同。

采用叠加法时，上图的朝向满足起手要求。

U形态复原公式：

进阶公式二 F (R U R' U') F'

起手时，两个黄色面朝左，与叠加法的起手是不同的。

L

L形态中，两个未还原的角块相对。

采用叠加法时，上图的朝向满足起手要求。

L形态复原公式：

进阶公式三 (F R' F' R) (U R U' R')

起手时，俯视图中左下角的黄色面朝下。

零个黄色面已还原

所有的黄色面都未还原的情形有2种。其叠加法如下：无论哪种情形，保证俯视图中左侧的两个角块是黄色朝左的:

然后使用公式一，就一定转为As形态，从而通过公式一解决。

H

H形态中，四个未还原黄色面朝向两个方向。

对于叠加法，首先保证俯视图中左上角的角块黄色朝上，上图已满足要求。

然后，执行两次公式一。这里，中途不需要转动U层调整朝向。

消步后即为H形态的复原公式：

进阶公式四 (R' U' R U') (R' U R U') R' U2 R

Pi

Pi形态中，四个未还原黄色面朝向三个方向。

采用叠加法时，上图的朝向满足起手要求。

Pi形态复原公式：

进阶公式五 F (R U R' U')2 F'

叠加法原理（选读）

所有的情形都能通过执行一次As的复原公式（公式一），转化为As或S，也就是恰有一个黄色面已还原的情形。但我们对初始的朝向做了要求，并不是随便做一次公式一就一定能转化。那么，为什么我们提供的朝向就能奏效呢？

以T形态为例。它属于两个黄色面已还原的情形，我们要求俯视图中左上角的角块黄色朝上，然后执行公式一，完成转化。

对于As形态，我们要求俯视图的左上角的角块黄色面已复原，然后执行公式一，完成复原。

比较这两个俯视图，可以发现除了左下角的角块黄色面都朝下外，其他三个角块的形态都不同。因此同样执行公式一后，也会有三个角块的形态不同。既然执行结束后，As形态的四个黄色面都复原，那么T形态一定转化为恰有一个黄色面已还原，即As或S。你可以对叠加法图中左边5个形态的朝向做验证，它们一定恰好有一个角块的形态与As相同。

As形态执行公式一后，不会改变左上角的角块的状态（但会改变位置）。因此T形态执行公式一后，左上角的角块的状态也不会改变，其状态与S形态的三个未复原的角块一致，因此推断出转化为S形态。同理，所有的两个黄色面已还原的情形，都将转化为S形态。

四角归位

这步将顶层的四个角块的相对位置也还原正确。

观察顶面的四个侧面，有两种可能的情况：

一侧的角块颜色相同

如图所示，一个侧面的角块颜色相同，其余三个侧面的颜色不同。这里画出的是橙色相同。

Ux将角块颜色相同的侧面转向左侧，然后完成公式：

公式三 (R U R' U') R' F (R2 U' R' U') (R U R' F')

如果你在上一节只记忆了公式〇（R' U L U' R U L'），并不打算记新的公式，那么Ux将角块颜色相同的侧面转向后侧，然后完成：

L F (公式〇) U' F' L'

每侧的角块颜色不同

如图所示，任何一侧的角块颜色都不同。此时每一侧都是等价的，因此无需做方向调整。

可以叠加公式三解决：执行一次公式三（或是L F (公式〇) U' F' L'），使之变为上一种情形。

一步复原公式为：

进阶公式六 F (R U' R' U') (R U R' F') (R U R' U') (R' F R F')

后六棱

目标

这步的目标是将剩下的6个棱块（以灰色标出）复原，从而复原整个魔方。后六棱又叫做LSE(Last Six Edges)、L6E。

与CMLL类似，我们将后六棱分为两个步骤：

一. 后六棱色向

这步(eo/4a)要将顶层和底层上剩余的块的色向还原正确，也就是白色和黄色一致朝上或朝下。下面是一个色向还原的例子。

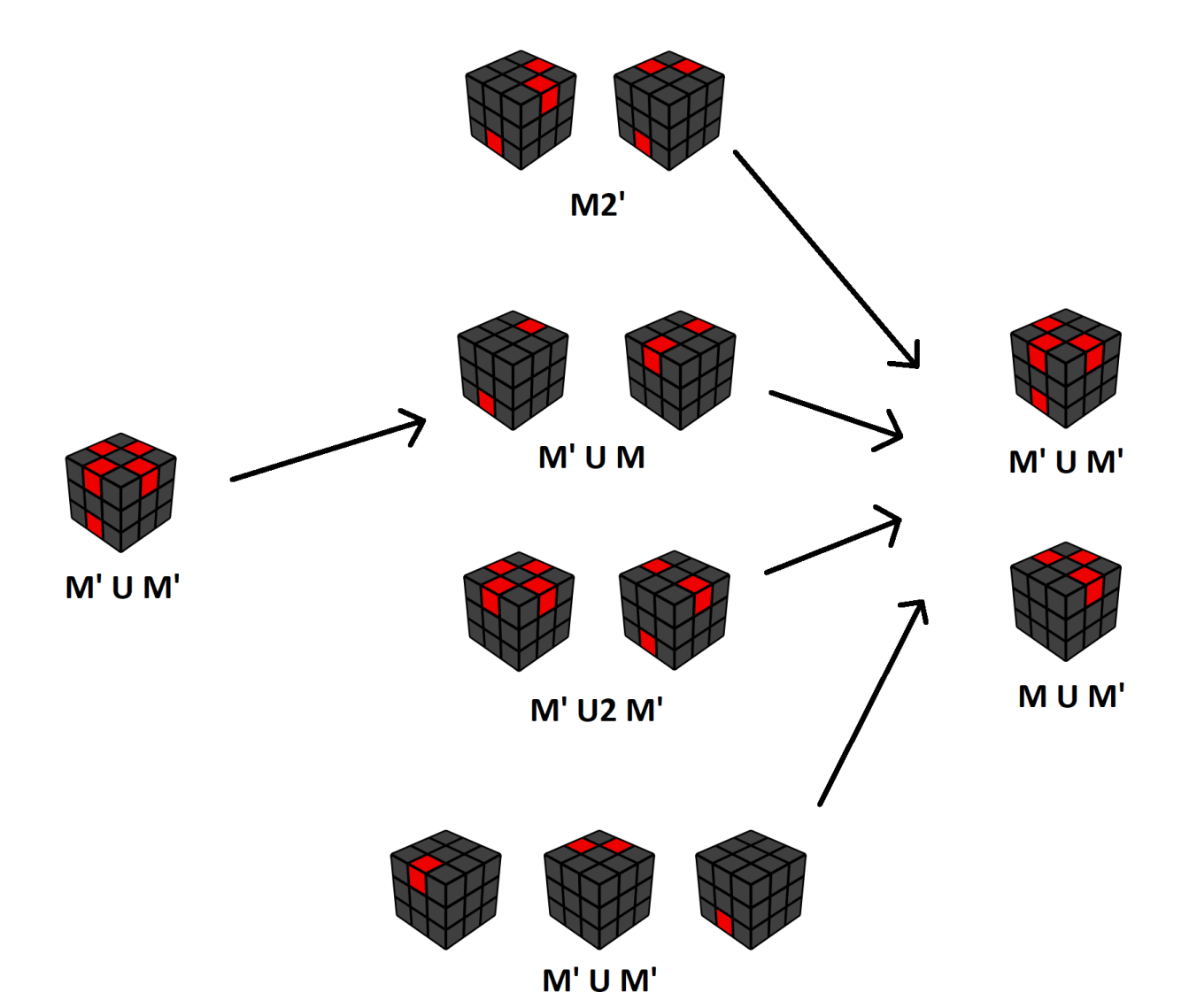
色向复原流程

色向的复原流程如下：（图片作者：甘浩東/Anto Kam）

在这张图中，中心块的色向已经复原；红色棱块代表色向错误的棱块，即白色/黄色面不朝向上/下。

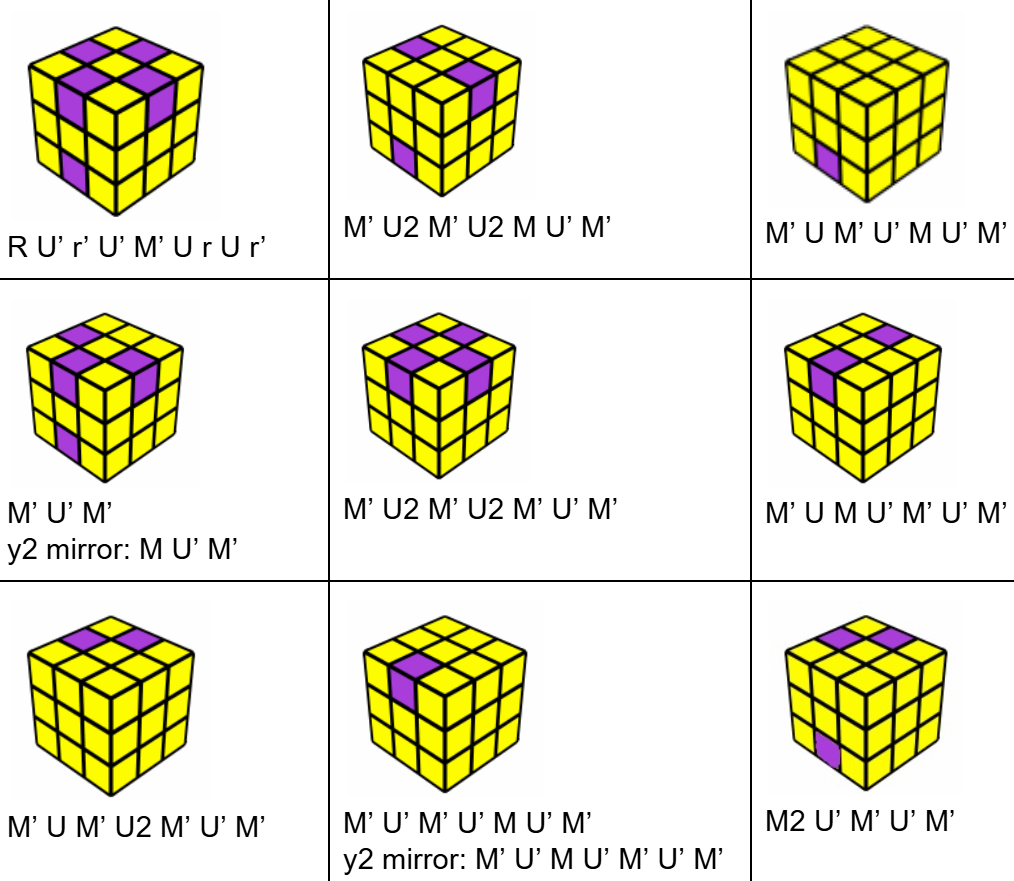
色向复原公式

色向直接复原的公式如下：（图片作者：Kian Mansour）

在这张图中，中心块的色向已经复原；紫色棱块代表色向错误的棱块。

无论采用哪一种学习路径，我们都建议结合四种基本操作来辅助理解。

二. 后六棱归位

这步要在色向还原的基础上，将剩下的6个棱块彻底复原，从而完成整个魔方的复原。可以细分为左右棱归位(ulur/4b)和后四棱(l4e/4c)。

左右棱归位步骤

先将左右面位于顶层的2个棱块复原。先将它们都移动到底层，再插入：

在这张图中，紫色代表要插入的两个棱块，即黄蓝黄绿棱块。

后四棱公式

复原M层的最后4个棱块：

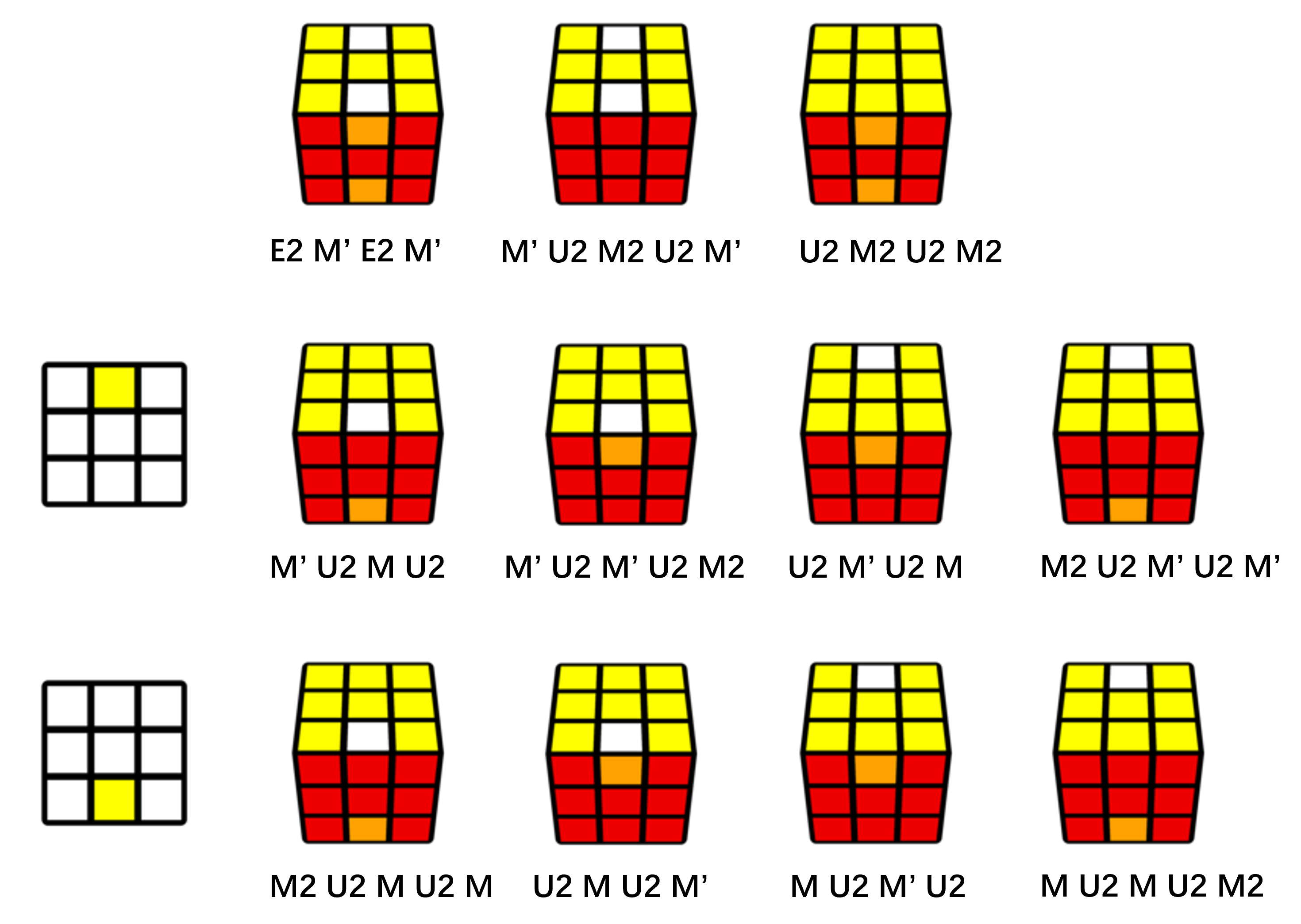
后八类情形都属于三个棱块未复原（三棱换）的情形。仅通过观察U层和F层不足以确定其形态，还需要观察D层的形态（图片左侧）。

三棱换的公式不必全部记忆，在对应小节中将介绍一种不依赖转体的理解性的复原方法。另外，利用x转体可以将三棱换归为两种情形，即顺时针和逆时针三棱换。

如此就完成了整个魔方的复原。

后六棱的两个步骤的具体内容将在以下两节介绍。

后六棱色向

目标

这步要将顶层和底层上剩余的块的色向还原正确，主要解决的是剩下6个棱块的色向。这步又叫做EO (Edges Oriented)。

“色向”这个词在CMLL中已经提及过。所谓块的色向(orientation)，在这里指的是块沿着上下方向的朝向。例如，某个块含有黄色面，在其朝向正确时，黄色面是向上的。而在它色向正确时，黄色面不仅可以朝上，还可以朝下。

以下是一个色向还原正确的具体例子。你可以拖动魔方，查看底层的状态：

在下图中，色向错误的棱块数量为4。（注意底层也有两个。）

对于这种情形的抽象表示，我们只标出上下两层中，色向错误的棱块面的位置，使用红色表示。它不一定代表真正的红色面。

中心块的色向通过一步Mx就能解决，我们先还原它们，再处理剩下6个棱块的色向。

没有必要将中心块完全对齐。对于黄色中心块，它在顶层或底层都是一样的。

为了方便，我们称色向错误的棱块为坏块，色向正确的棱块为好块。

基本操作

我们介绍两类基本操作。

基本操作三、四为一类，主要作用是改变4个棱块的色向，其中3个位于顶层，1个位于底层。

基本操作五、六为一类，作用是交换上下层各1个棱块的位置，但不改变色向。

基本操作三： `M' Ux Mx`

这里，Ux被限制为U或U'，Mx也被限制为M'或M，因此共有4种组合。其作用是改变除UB、DB两个位置外，其余的4个棱块的色向：

或者：

等等。可以看到执行完基本操作三后，4个红色面都从上/下面移向了侧面，意味着其对应棱块的色向已改变。当这4个棱块都是“坏块”时，执行操作后会都变为“好块”。

相应地，如果对应棱块是“好块”，执行操作后会变为“坏块”：

因此，这类基本操作能够改变“坏块”的总数量。如果对应的4个棱块恰好有x个“坏块”、(4 - x)个“好块”，那么执行操作后，这4个棱块将恰有(4 - x)个“坏块”，总体数量的变化为(4 - x) - x = 4 - 2x。除非x = 2，否则操作一定会改变“坏块”的总数。例如，如果这四个位置有1个色向错误，那么执行完后这四个棱块变为3个色向错误，总数量加2。